StackGP.fitness

fitness is a StackGP function that computes the \(1-r^2\) for a GP model. This is the default accuracy measure used in search.

The function expects 3 arguments: model, inputData, and response

The arguments are described below:

• model: A StackGP model.

• inputData: A numpy array containing the input data used to evaluate the model.

• response: The ground truth response to compare the model’s response to.

---

First we need to load in the necessary packages

import StackGP as sgp
import numpy as np

Overview

Computing fitness for a random model

Here we generate a random model with up to 4 variables, the default operator set, the default constant set, and a maxSize of 10.

randomModel=sgp.generateRandomModel(4, sgp.defaultOps(), sgp.defaultConst(), 10)

We can display the random model below

sgp.printGPModel(randomModel)

\[\displaystyle 2.02581370493437 \left(- 0.70258722293364 x_{0} - 0.70258722293364 x_{3} - 1\right)^{2} - 5.71828182845904\]

Now we generate a random input dataset and a ground truth response vector.

inputData = np.random.rand(4, 100) 
response = np.sin(inputData[0]) + np.cos(inputData[1]) + inputData[2]**2 - inputData[3]**3

Now we can compute the RMSE between the model’s response and the ground truth response.

sgp.fitness(randomModel, inputData, response)

0.9996068366284323

---

---

Examples

This section provides some interesting examples to demonstrate how fitness can be used.

---

Checking error of best evolved model

Likely, we are interested in determining the quality of the best model evolved on a test set.

Lets start by generating a training and test set with 4 features.

trainInputData = np.random.rand(4, 100)
trainResponse = 5*trainInputData[0] + 2*trainInputData[1] + trainInputData[2]**2
testInputData = np.random.rand(4, 100)
testResponse = 5*testInputData[0] + 2*testInputData[1] + testInputData[2]**2

Now lets evolve a model population using the training data.

models=sgp.evolve(trainInputData, trainResponse, tracking=True, generations=200, elitismRate=10, tourneySize=30)

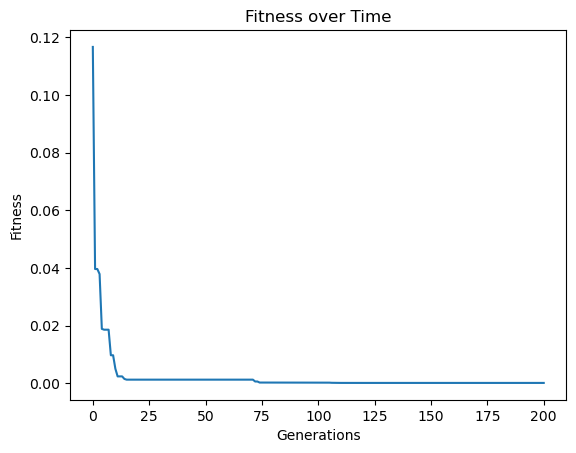
Now lets pick the best model evolved from the population.

bestModel = models[0]
sgp.printGPModel(bestModel)

\[\displaystyle 5.01025360413344 x_{0} + 1.99447659663629 x_{1} + 1.63393325099573 \sqrt{e^{x_{2}^{2}}} - 1.61881544923791\]

Now lets evaluate the fitness of the best model on the test set.

sgp.fitness(bestModel, testInputData, testResponse)

0.00014515275259152638

We can compare that to the fitness on the training set to see if we were overfitting the training or performing similarly on both sets.

sgp.fitness(bestModel, trainInputData, trainResponse)

0.00013148639667670547

Using fitness as a Fitness Objective

\(1-r^2\) is the default fitness function and is used as the accuracy objective in search. Here we demonstrate how we can use just fitness rather than the default of using fitness and stackGPModelComplexity. This converts the search to a 1D problem rather than a 2D optimization problem.

We will use a randomly generated model to generate the response. So we start with generating a random model.

randomModel=sgp.generateRandomModel(4, sgp.defaultOps(), sgp.defaultConst(), 20)
sgp.printGPModel(randomModel)

\[\displaystyle e^{- \frac{9.39861563290544}{x_{1}}}\]

Now we can generate some data and use the above random model to generate the response from the random input data.

inputData = np.random.rand(4, 100)
response = sgp.evaluateGPModel(randomModel, inputData)

Now we can evolve models to fit the generated training data. We will set just fitness as the fitness objective rather than stackGPModelComplexity and fitness.

models = sgp.evolve(inputData,response, tracking=True, modelEvaluationMetrics=[sgp.fitness])

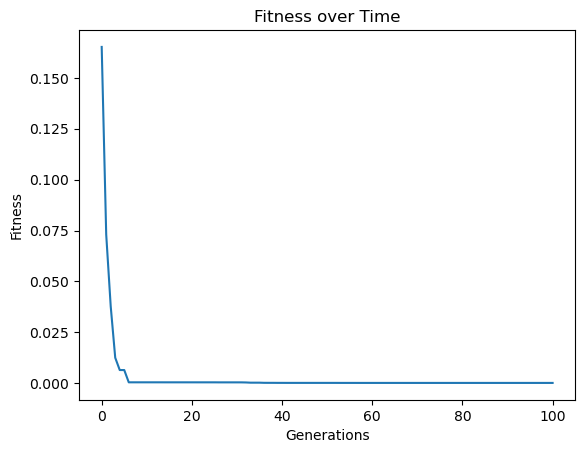
Now we can look at the best model generated.

sgp.printGPModel(models[0])

\[\displaystyle 9.62143970076573 \cdot 10^{-5} x_{1}^{10} - 9.62143970076573 \cdot 10^{-5} e^{\frac{0.00987976710843726}{\left(1 - 0.0993970176033329 e^{2 x_{1}}\right)^{2}}} + 9.76969226624036 \cdot 10^{-5}\]

Now we can check how well it generalizes to test data. First we need to generate the test data.

testInputData = np.random.rand(4, 100)
testResponse = sgp.evaluateGPModel(randomModel, testInputData)

Now we can compute the fitness on the test data.

sgp.fitness(models[0], testInputData, testResponse)

9.710930943729323e-05

We can also visualize the quality of predictions on the test data.

sgp.plotModelResponseComparison(models[0], testInputData, testResponse)

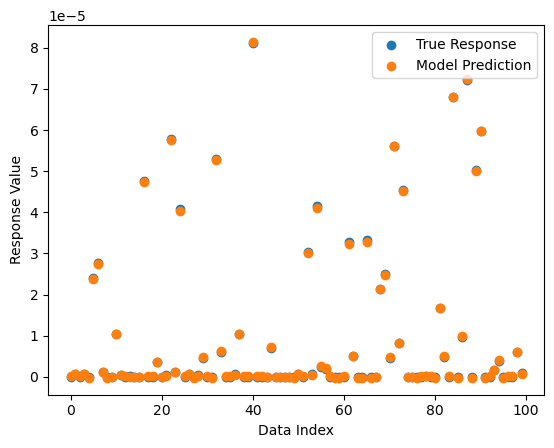
To make it easier to see how close the values are to the test values, we can visualize the residual plot.

sgp.plotModelResiduals(models[0], testInputData, testResponse)

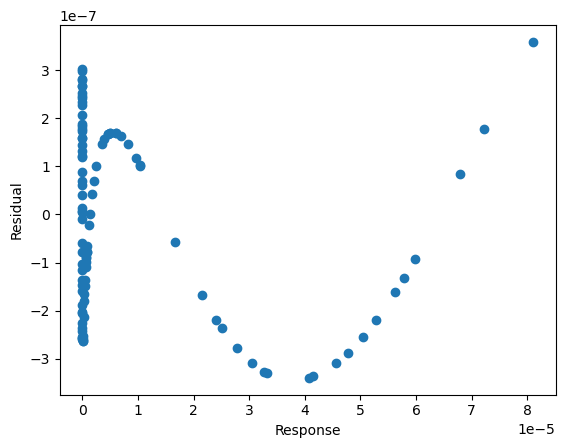
Updating Embedded Objectives in Evolved Model

We may be interested in updating the embedded fitness values in a model using a new set of data for analysis. We can easily do this with the setModelQuality function.

First we need to generate some models and data.

inputData = np.random.rand(5, 100)
randomModel = sgp.generateRandomModel(5, sgp.defaultOps(), sgp.defaultConst(), 20)
response = sgp.evaluateGPModel(randomModel, inputData)
sgp.printGPModel(randomModel)

\[\displaystyle e^{e^{3.14159265358979 \sqrt{\left(1 - 0.318309886183791 x_{1}\right)^{2}}}}\]

Now lets train a model using the standard search objectives.

models = sgp.evolve(inputData, response, tracking=True)

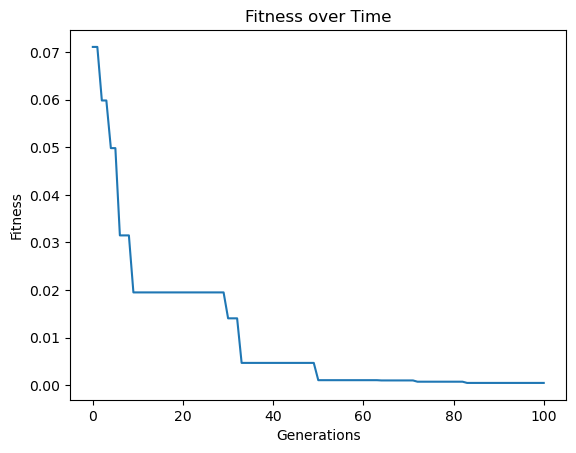
Now we can generate a test set.

testInputData = np.random.rand(5, 100)
testResponse = sgp.evaluateGPModel(randomModel, testInputData)

Now we can upate the model embedded model quality objectives to include \(1-r^2\) with respect to the test set.

for model in models: 
    sgp.setModelQuality(model, testInputData, testResponse, [sgp.fitness])

Now we can look at the fitness vector of a model and we can see it contains 1 value (\(1-r^2\)).

display(sgp.printGPModel(models[0]))
print("Fitness vector: ", models[0][-1])

\[\displaystyle 10060532.5698567 + 1.47269743762274 \cdot 10^{19} e^{- 21.0257011904559 e^{x_{1}}}\]

Fitness vector:  [0.0004399535860304393]