StackGP.stackGPModelComplexity

stackGPModelComplexity is a StackGP function that computes the combined stack length for a GP model. This is the default complexity measure used in search.

The function expects 1 argument: model

The argument is described below:

• model: A StackGP model.

---

First we need to load in the necessary packages

import StackGP as sgp
import numpy as np

Overview

Computing complexity for a random model

Here we generate a random model with up to 4 variables, the default operator set, the default constant set, and a maxSize of 10.

randomModel=sgp.generateRandomModel(4, sgp.defaultOps(), sgp.defaultConst(), 10)

We can display the random model below

sgp.printGPModel(randomModel)

\[\displaystyle x_{1} + x_{2} - 0.865255979432265\]

Now we can compute the model complexity

sgp.stackGPModelComplexity(randomModel)

7

---

---

Examples

This section provides some interesting examples to demonstrate how stackGPModelComplexity can be used.

---

Checking complexity of best evolved model

Likely, we are interested in determining the complexity of models evolved.

Lets start by generating a training and test set with 4 features.

trainInputData = np.random.rand(4, 100)
randomModel = sgp.generateRandomModel(4, sgp.defaultOps(), sgp.defaultConst(), 10)
display(sgp.printGPModel(randomModel))
trainResponse = sgp.evaluateGPModel(randomModel, trainInputData)

\[\displaystyle \sqrt{x_{2} \left(7.36591123815405 - x_{1}^{2}\right)}\]

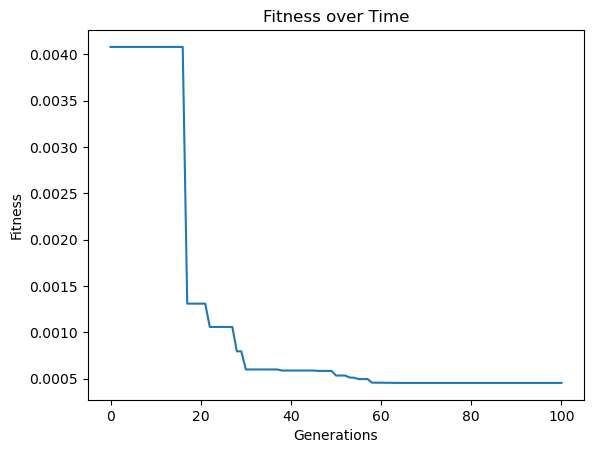
Now lets evolve a model population using the training data.

models=sgp.evolve(trainInputData, trainResponse, tracking=True)

Now lets pick the best model evolved from the population.

bestModel = models[0]
sgp.printGPModel(bestModel)

\[\displaystyle - 0.123761055868954 x_{1}^{2} + 2.64444723491903 \sqrt{x_{2}} + 0.0476920384907215\]

Now lets evaluate the complexity of the best model.

sgp.stackGPModelComplexity(models[0])

11

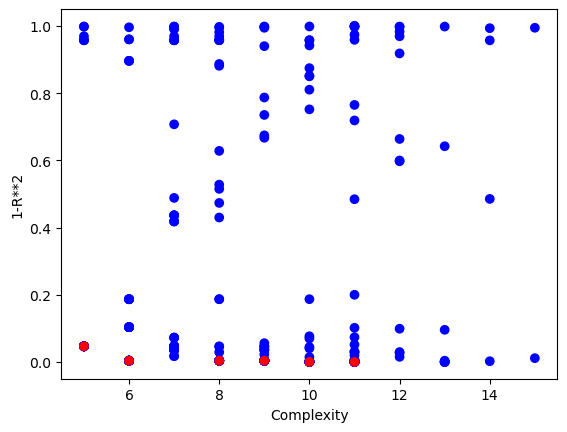
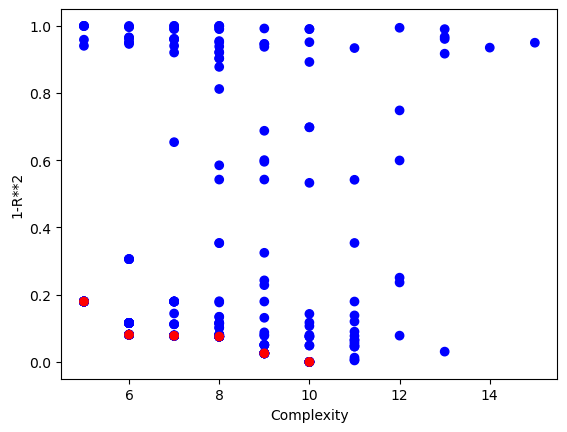
We can also visualize the Pareto front plot of the model population to see the complexity-accuracy trade-off of all models in the population.

sgp.plotModels(models)

Using stackGPModelComplexity as a Fitness Objective

The default fitness objectives used during search are fitness and stackGPModelComplexity. Here we show how to manually specify using stackGPModelComplexity, although, in practice it isn’t necessary.

We will use a randomly generated model to generate the response. So we start with generating a random model.

randomModel=sgp.generateRandomModel(4, sgp.defaultOps(), sgp.defaultConst(), 20)
sgp.printGPModel(randomModel)

\[\displaystyle x_{3}^{2} \left(x_{2} + x_{3}\right)\]

Now we can generate some data and use the above random model to generate the response from the random input data.

inputData = np.random.rand(4, 100)
response = sgp.evaluateGPModel(randomModel, inputData)

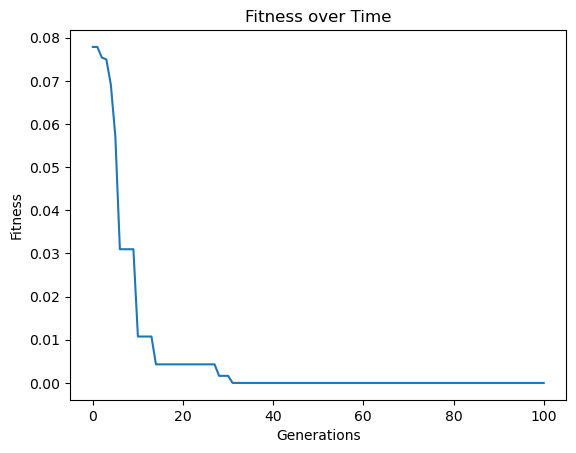
Now we can evolve models to fit the generated training data. We will manually set fitness and stackGPModelComplexity as the fitness objectives.

models = sgp.evolve(inputData,response, tracking=True, modelEvaluationMetrics=[sgp.fitness, sgp.stackGPModelComplexity])

Now we can look at the best model generated.

sgp.printGPModel(models[0])

\[\displaystyle 1.0 x_{3}^{2} \left(x_{2} + x_{3}\right) + 1.6678451248621 \cdot 10^{-17}\]

Now we can view the complexity of that best model.

sgp.stackGPModelComplexity(models[0])

10

We can also view the Pareto front plot of the evolved model population to see the complexity-accuracy trade-off of all models in the population.

sgp.plotModels(models)

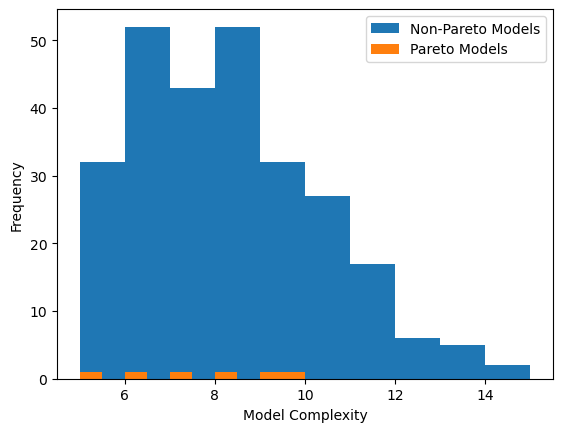
We could also plot the complexity distribution in the population.

sgp.plotModelComplexityDistribution(models)